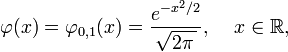There are various ways to characterize a probability distribution. The most visual is the probability density function (PDF). Equivalent ways are the cumulative distribution function, the moments, the cumulants, the characteristic function, the moment-generating function, the cumulant-generating function, and Maxwell's theorem. See probability distribution for a discussion.
To indicate that a real-valued random variable X is normally distributed with mean μ and variance σ² ≥ 0, we write
While it is certainly useful for certain limit theorems (e.g. asymptotic normality of estimators) and for the theory of Gaussian processes to consider the probability distribution concentrated at μ (see Dirac measure) as a normal distribution with mean μ and variance σ² = 0, this degenerate case is often excluded from the considerations because no density with respect to the Lebesgue measure exists.
The normal distribution may also be parameterized using a precision parameter τ, defined as the reciprocal of σ². This parameterization has an advantage in numerical applications where σ² is very close to zero and is more convenient to work with in analysis as τ is a natural parameter of the normal distribution.
The continuous probability density function of the normal distribution is the Gaussian function
where σ > 0 is the standard deviation, the real parameter μ is the expected value, and
is the density function of the "standard" normal distribution: i.e., the normal distribution with μ = 0 and σ = 1. The integral of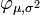 
over the real line is equal to one as shown in the Gaussian integral article.
As a Gaussian function with the denominator of the exponent equal to 2, the standard normal density function 
is an eigenfunction of the Fourier transform.
The probability density function has notable properties including:
- symmetry about its mean μ
- the mode and median both equal the mean μ
- the inflection points of the curve occur one standard deviation away from the mean, i.e. at μ − σ and μ + σ.
Reference : http://en.wikipedia.org/wiki/Normal_distribution
